Digital Logic 2

4. Karnaugh map

For purposes of simplification,the Karnaugh map is a convenient way of representing a Boolean function of a small number (up to four to six) of variables.The map is an array of 2ᵑ squares,representing the possible combinations of values of n binary variables.

Once of the map of a function is created,we can often write a simple algebraic expression for it by noting the arrangement of the 1s on the map.The principle is as follows:Any two squares that are adjacent differ in only one of the variables.If two adjacent squares both have an entryof one,then the corresponding product terms differ in only one variable.

OUTPUT = WY̅+Z+W̅XY+W̅YZ̅+WX̅YZ̅

OUTPUT=XY̅Z̅+X̅Z+X̅Y

OUTPUT=Y̅Z̅+W̅YZ+W̅XY

The diagram below illustrates the correspondence between the Karnaugh map and the truth table for the general case of a two variable problem. 

 The values inside the squares are copied from the output column of the truth table, therefore there is one square in the map for every row in the truth table. Around the edge of the Karnaugh map are the values of the two input variable. A is along the top and B is down the left hand side. The diagram below explains this: 

The values around the edge of the map can be thought of as coordinates. So as an example, the square on the top right hand corner of the map in the above diagram has coordinates A=1 and B=0. This square corresponds to the row in the truth table where A=1 and B=0 and F=1. Note that the value in the F column represents a particular function to which the Karnaugh map corresponds.

Example

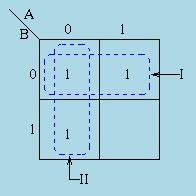
Consider the expression Z = f(A,B) = A̅B̅ + AB̅ + A̅B plotted on the Karnaugh map: 

Pairs of 1's are grouped as shown above, and the simplified answer is obtained by using the following steps:

Note that two groups can be formed for the example given above, bearing in mind that the largest rectangular clusters that can be made consist of two 1s. Notice that a 1 can belong to more than one group.
The first group labelled I, consists of two 1s which correspond to A = 0, B = 0 and A = 1, B = 0. Put in another way, all squares in this example that correspond to the area of the map where B = 0 contains 1s, independent of the value of A. So when B = 0 the output is 1. The expression of the output will contain the term B̅.

For group labelled II corresponds to the area of the map where A = 0. The group can therefore be defined as A̅. This implies that when A = 0 the output is 1. The output is therefore 1 whenever B = 0 and A = 0 

Hence the simplified answer is Z = A̅ + B̅

Summary

We can summarize the rules for simplification as follows:

      1.       Among the marked squares, find those that belong to a unique largest block of either 1, 2, 4 or 8 and circle those blocks.

      2.       Select additional blocks of marked squares that are as large as possible and as few in number as possible, but include every marked square at least once. The results may not be unique in some cases. For example, if a marked square combines with exactly two other squares, and there is no fourth marked square to complete a larger group, then there is a choice to be made as two groupings to choose. When you are circling groups, you are allowed to use the same 1 more than once.

      3.       Continue to draw loops around single marked squares, or pairs of adjacent marked squares or groups of four, eight, etc. in such a way that every marked square belongs to at least one loop; then use as few of these blocks as possible to include all marked squares.

     Written by Ng Wui Sheng (B031210031)